The Dark Knight (2008) Through The Lens of Game Theory (part 1)

The application of game theory, with Batman, The Joker among the players, can be used to understand the moral themes of the Dark Knight (2008). Characters show their complexity through their decisions and frequent opposition to rationality throughout the film.

[Nick is a Bachelor of Economics student who enjoys how economics can help people understand the world through decision-making. He minors in mathematics and film and screen studies and is trying to grasp connections between the widely opposing disciplines.]

Chaos, order, anarchy, vigilantism, corruption, faith, and immovable objects pervade The Dark Knight (2008). The gritty underground war between the police and mafia are taken over by the championing superpowers; Batman upholds what is decent and delivers what the city deserves. On the bad guys' side stands The Joker himself in all his games of unpredictability, its twisted outcomes bending to reveal single will: that Gotham City can be corrupted.

Viewing pivotal scenes through the lens of game theory can provide a tangible blueprint to give motive to the characters' strategic decision-making, namely in the following scene:

Two ships, one of criminals and the other with civilians, are given the remote control to blow up the other and save themselves, or they will be blown up. If neither boat makes a move by midnight, The Joker blows them both up.

The Joker presents a variation of the classic Prisoner's Dilemma, which goes as follows:

Two criminals are arrested and put in different rooms. They each have the option to either betray the other and walk away free (0 years) while the other is jailed for a very long time (10 years), or stay silent. If both criminals stay silent, they go to jail for a short time (1 year), however, if both of them betray one another, they get a moderate jail time (6 years).

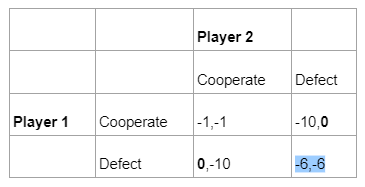
Note: payoffs are listed as (Player 1, Player 2).

Each criminal is concerned with maximising their payoff, that is, to obtain the least amount of time served. If Player 2 chooses to cooperate, a rational Player 1 would betray the other (that is, to Defect as 0>-1). He would also choose Defect if Player 2 plays Defect (as 0>-1). Player 1's dominant strategy is to play Defect and betray the other person, and by symmetry, Player 2 is the same. Thus the Nash Equilibrium will be (Defect, Defect). It is worse off for both players, serving 6 years of jail each.

Tragically, the outcome to both cooperate is strategically inferior. In this simultaneous-move game, the criminals must assume the worst from the other, yet being cooperative yields the best total outcome for both players.

Now the Joker's twist is that if both parties cooperate, at midnight he detonates both ships.

Note: payoffs are listed as (Ship 1, Ship 2).

The logical move for Player 2 will be to play Defect to protect themselves, as doing nothing will lead to being blown up by the other ship, or eventually by The Joker. Detonating is the dominant strategy for both ships.

"So who's it going to be - Harvey Dent's most wanted scumbag collection… or the sweet innocent civilians?"

The pilot of the prisoner ferry looks down at the remote in his hands. Prisoners begin yelling and pushing. The guards level their weapons at the crowd. A similar chaos happens in the civilian boat. They decide to hold it to a vote, the vast majority opting to detonate the other boat.

A huge, tattooed prisoner steps up to the warden, who is frozen by the weight of his responsibility. He gives the prisoner the remote, and to everyone's surprise, the menacing giant rids the option of detonating by throwing it out of the window. The criminals should be the ones taking the hit, argues one civilian as he slowly grabs the controller. But still, at the last second, he falters and is not able to detonate the other ship. Both ships cooperate and thankfully, Batman stops The Joker from pressing his button at midnight.

The morality of both ships made them deviate from their rational behaviour. Indeed, the civilians voted logically, but no one can act. From the scum of Gotham's most wanted and upper class arises not corruption, but their humanity, and the Joker loses.

Stay tuned for part two coming out soon!

References

1. Arbesman, Samuel. “The mysterious equilibrium of zombies and other things mathematicians see at the movies.” The Best Writing on Mathematics 2010, 31 Dec. 2011, pp. 383–386, https://doi.org/10.1515/9781400836123-035.
2. Chwe, Michael Suk-Young. Jane Austen, Game Theorist, 23 Mar. 2014, https://doi.org/10.23943/princeton/9780691162447.001.0001.
3. Geerling, Wayne, et al. “Using squid game to teach game theory.” Journal of Economics Teaching, 2023, pp. 47–63, https://doi.org/10.58311/jeconteach/2dfaffe5f7d50d5513a89ae4be17f4d9ff8cc3f3.
4. “Networks.” Game Theory in The Dark Knight : Networks Course Blog for INFO 2040/CS 2850/Econ 2040/SOC 2090, blogs.cornell.edu/info2040/2021/09/19/game-theory-in-the-dark-knight-4/. Accessed 15 Apr. 2024.
5. Nolan, Christopher, director. The Dark Knight. Warner Brothers, 2008.
6. O’Roark, Brian, and William Grant. “Games superheroes play: Teaching game theory with comic book favorites.” The Journal of Economic Education, vol. 49, no. 2, 14 Mar. 2018, pp. 180–193, https://doi.org/10.1080/00220485.2018.1438861.