[Nick is a Bachelor of Economics student who enjoys how economics can help people understand the world through decision-making. He minors in mathematics and film and screen studies and is trying to grasp connections between the widely opposing disciplines.]

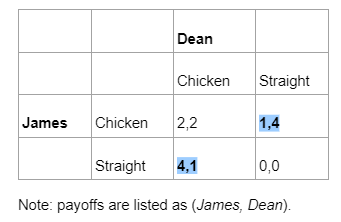
The game of chicken is explored in the Joker’s attempts to corrupt Batman by targeting to break his one rule – to not kill. Each player can stand their ground or chicken out, and as per the classic example of James and Dean, precisely one player is expected to be chicken in the mixed-strategy Nash Equilibrium: to play Chicken half the time, and Straight in other times.
“Hit me. Come on. I want you to hit me,” demands the Joker as Batman speeds towards him on the Bat-pod. The Joker uses his gun not to shoot back but only to clear Batman’s way of cars, to be an unmissable target.
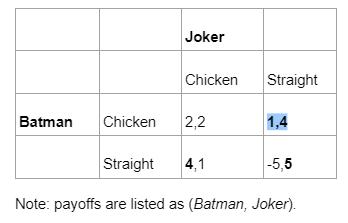
What is different with James and Dean’s classic mixed-strategy scenario is that if the outcome is (Straight, Straight), that is, Batman lethally knocks The Joker down in the scenario, Batman breaks his one rule and this is terrible for him (-5 utility). The Joker, in all his madness, would succeed in breaking Batman’s one rule (gaining 5 utility, though in the afterlife), and further, he knows this will not happen. Thus The Joker plays Straight, a pure dominant strategy, and the only remaining Nash equilibrium is (Chicken, Straight).
Batman roars in his face but at the last second yields and swerves around The Joker, slams into a wall and is rent unconscious.
The Joker also senses Batman’s affection for Rachel Dawes is placed with more importance than protecting Gotham’s anti-corruption attorney Harvey Dent, the city’s white knight. He traps Batman with a choice to save one or the other from separate burning buildings. Batman gets 1 utility from choosing to save Harvey but losing Rachel, much to his devastation. The Joker gets 3 utility from seeing Batman’s anguish, and only 1 from Rachel being saved and Harvey dying. He wants to use Harvey and not kill him.
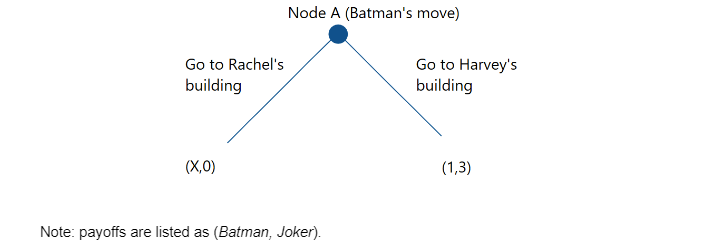
Let X denote Batman’s utility for keeping Rachel alive. Only Batman knows this value, but the Joker can form a belief.* He guesses it is rather high from the way “[Batman] threw [him]self after her” as The Joker threw Rachel out of a skyscraper. It turns out, X>1 and just as expected, Batman prizes saving his love higher than saving Dent.
But there is a twist: the addresses are mixed up and it is a game of imperfect information. In a blitz of panic and rage, he believes he is playing at Node A and does not consider the possibility of being at Node B, having bounded rationality. He chooses to Save Rachel, but only finds Harvey, and Rachel dies. Batman chose the safety of Rachel over Dent, who is far more important to Gotham. The payoff is Batman loses Rachel. The Joker wins (and also escapes captivity).
The mixed-strategy equilibrium is {(Harvey, Rachel); (Switch)}.

In fact, Rachel had just accepted Harvey’s marriage proposal in her last moments. As revenge, Dent turns into the villain Two-Face and begins a killing spree among the corrupt officers and Mafia. He kidnaps police commissioner Gordon’s family, blaming his negligence for Rachel’s death. As he points the gun at Gordon’s son, Batman hurls himself at Dent and throws him off a building, killing him and saving the child. Because of the Joker’s final ace in the hole, Batman finally breaks his one rule.
But Gotham must never know the truth about Dent’s crimes. The Joker proved that Gotham’s white knight could fall from grace and become a villain. Batman decides to take the blame for all of Dent’s killings, thereby preserving his public image as a symbol of hope for a Gotham rid of corruption.

Unlike the previous game between Dent and Rachel, Batman chooses to save Dent over what is nicer for him. And it is fitting that the people who showed their awesome humanity on the two ships mourn Dent as a hero, persisting to resist The Joker’s anarchy. And Batman knows it is worth breaking his rule and image for Gotham’s soul. He’s the hero Gotham deserves, but not the one it needs right now.
There are many disciplines to analyse and appreciate the movie’s themes and characters. I feel that game theory’s universality is under-appreciated, and hope this article forms an inkling from which other applications of game theory can be enjoyed.
See more on What Game Theory Reveals About Life, The Universe, and Everything.
- see Bayesian Nash Equilibrium for forming beliefs in uncertainty
References
- Arbesman, Samuel. “The mysterious equilibrium of zombies and other things mathematicians see at the movies.” The Best Writing on Mathematics 2010, 31 Dec. 2011, pp. 383–386, https://doi.org/10.1515/9781400836123-035.
- Chwe, Michael Suk-Young. Jane Austen, Game Theorist, 23 Mar. 2014, https://doi.org/10.23943/princeton/9780691162447.001.0001.
- Geerling, Wayne, et al. “Using squid game to teach game theory.” Journal of Economics Teaching, 2023, pp. 47–63, https://doi.org/10.58311/jeconteach/2dfaffe5f7d50d5513a89ae4be17f4d9ff8cc3f3.
- “Networks.” Game Theory in The Dark Knight : Networks Course Blog for INFO 2040/CS 2850/Econ 2040/SOC 2090, blogs.cornell.edu/info2040/2021/09/19/game-theory-in-the-dark-knight-4/. Accessed 15 Apr. 2024.
- Nolan, Christopher, director. The Dark Knight. Warner Brothers, 2008.
- O’Roark, Brian, and William Grant. “Games superheroes play: Teaching game theory with comic book favorites.” The Journal of Economic Education, vol. 49, no. 2, 14 Mar. 2018, pp. 180–193, https://doi.org/10.1080/00220485.2018.1438861.



