Trying to Mathematically(?) Prove That I am Not Performative

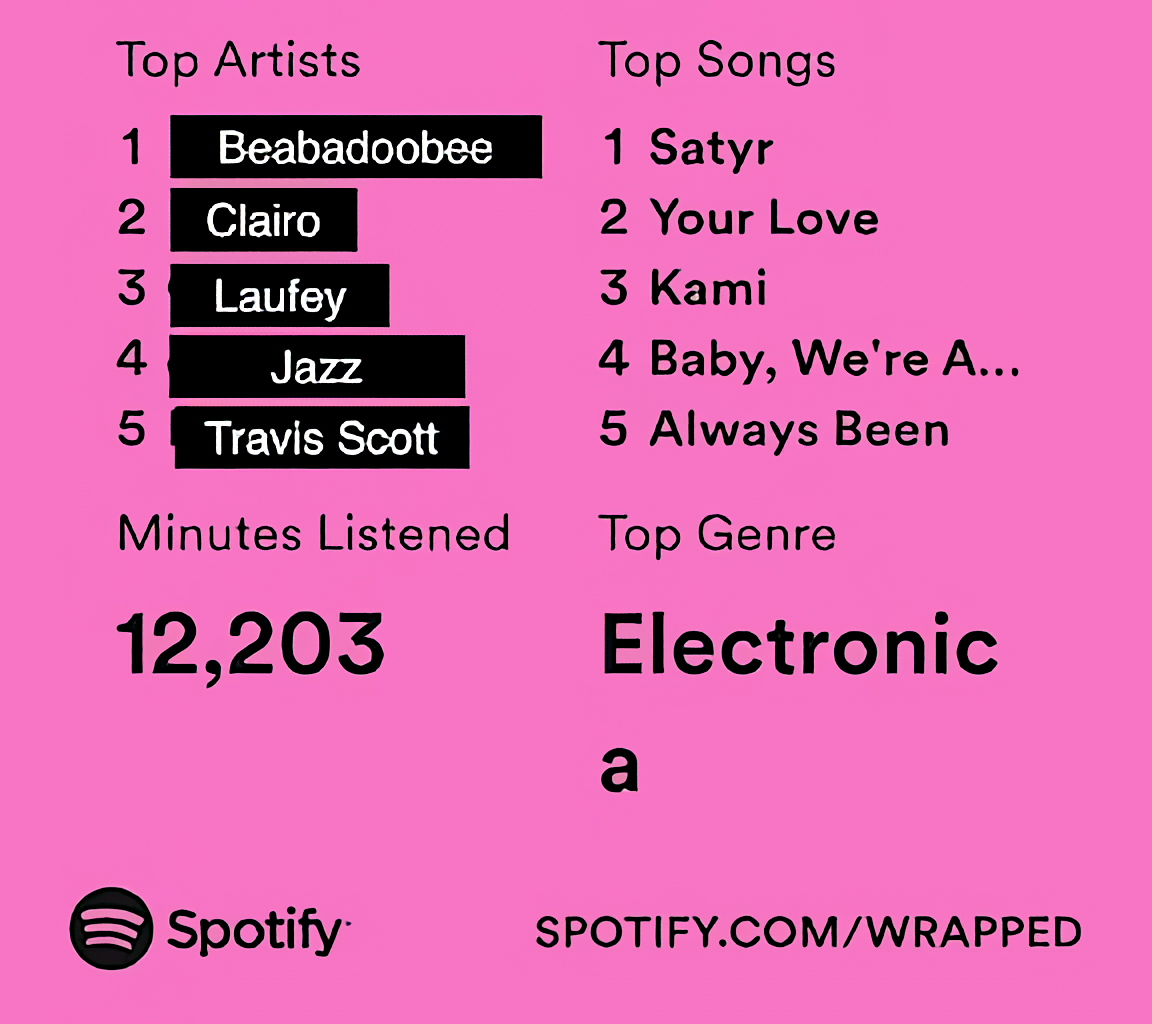
I swear I love Beabadoobee, but Spotify Wrapped got the receipts: 90% is house and Travis Scott. Lowkey hella performative – I know, but I’m going to try to mathematically(?) prove using WARP and Rationalisability, that I am in fact not performative.

[Dayabir is currently studying a Bachelor of Mathematics and Philosophy at Monash University. As a writer/editor, and an esteemed member of ESSA’s podcast team, Dayabir has a keen interest in probability, decision theory and their intersection with economics and consumer behaviour.]

Revealed Preferences 101

TLDR: We learn from actual observed choices and not by guessing.

Classic consumer theory starts with some sort of utility function, , and a budget . Revealed preferences (RP) flips this: Instead of specifying and hypothesising some , we instead observe choices (See [1]) often from ordinary market data, and we hope to god that these choices have come from some monotonic and concave utility function being maximised. The Weak, Strong and Generalised Axioms of Revealed Preference and Afriat’s Theorem makes this testable, even letting us construct a utility function nonparametrically if the data passes.

Mapping Spotify to RP – What’s the Good, Price & Budget?

Skip the Yap: Goods – Artists; Price – Time & Attention; Budget – Total minutes on Spotify in a year.

• Goods: We aggregate to artists (tracks/albums/playlists would also work). Let be the vector of minutes spent on each artist in period , where is a month in the Wrapped year.

• Price: Assuming the free version of Spotify, there isn’t a hard cost we can assign to the music. But we do have the opportunity cost: The cost of a 3 minute song is 3 minutes of your finite time, plus the cognitive effort of deciding to skip Katy Perry. Add in the horrid ads, and we can wrap up the attention costs nicely into a vector .

• Budget: Since we’ve decided that the Price is in time units, it only makes sense for the budget to follow suit. There’s minutes in the year, and wrapped tells you how much was ‘spent’. If you listened for 25,000 minutes, then that was the budget you allocated across the available goods (Artists). So then out Budget set, B, is all possible listening allocations I could have made with those 25,000 minutes. We let , be the total minutes listened in period t.

At face value, Wrapped is counts: top artist/tracks, most-played genres, minutes listened. If you picked, however unrealistically, Drake 300 times and The Weeknd only 50 times while both were available, you’ve revealed – given the constraints – a preference for spending minutes on Drake over The Weeknd. i.e. . 

 .

Then by the standard model, the choice each month solves:

Then let the dataset be . I.e. The collection of all observed Price, Budget and Choice triples of the T periods studied.

‘Proof’ Sketch:

We want to show that the set of choice structures O satisfies the Weak Axiom of Revealed Preference. I.e.

This proof actually is quite simple if you do the thing economists are infamous for: Assume Stuff.

A1: Stable tastes – A single, time-invariant, monotone, and concave u.

• Generally, musical tastes change. Not only across time, but also across contexts. My playlist for the gym My playlist for drinking iced matcha and reading feminist literature (6’4” btw). This would be a clear example of WARP being broken.

A2: Considerations Sets C are exogenous

• The true budget set is extremely large. If we consider the feasible budget set and choice architecture, then our subset is considerably smaller. Spotify tailors its suggestions to you, so the consideration set, , is in practice, heavily engineered. This is important since it implies that our preference results cannot be generalised to the whole of the Budget set, and only operates on .
• Skip the yap: The algorithm’s personalisation is accounted for in the price vector, not the utility.

A3: Singular Decision maker

• No sharing accounts

A4: Clean measurement

• reflects time costs and is the actual minutes listened.
• I.e. No accidental plays, accidental playing while sleeping, etc.

Under these assumptions, we can really just skip the math. If Spotify changes just the price, then I wouldn’t ever choose a distinct when is affordable, having previously chosen a distinct when was also affordable. So, WARP holds.

You might be thinking that I could’ve just said this from the start, and you’d be right. I could’ve just said this from the start.[3]

So… Am I performative?

Well, if passes WARP then a tidy interpretation is that my preferences are stable, and I prefer House and Travis Scott over Beabadoobee. But let’s be honest here, what are the chances of those assumptions actually holding. That’s right, it’s pretty much 0, I reckon we can conclude that I’m not performative and it was just the algorithm messing me up (Again, 6’4” btw).

To conclude, I’ve got no idea if this actually holds or if it’s all just yap. To be honest this was supposed to be an article about the economics of Spotify Wrapped and Asymmetrical Information. I don’t know how and when it became a ‘proof’. But yeah, read my previous article about why that weird kit kat flavor exists.

Footnotes

[1] Mas-Colell, Whinston, Green (1995), Microeconomic Theory, ch. 1–3.

[2] Rigotti (2024), GARP and Afriat’s Theorem, https://sites.pitt.edu/~luca/ECON3030/class%208.pdf 

[3] Apparently, I need more to show that the choices are rationalisable. By Afriat’s Theorem: Rationalisability GARP holds.

GARP:  [xjOxk][xkxj]

This can be proven by finding ut and t>0 such that s,t , usut+t(ptxs-xt)

This comes from solving: maxx0u(x) s.t. pxb and concavity, giving the Lagrangean: L(x,)=u(x)+(b-px).

Then I’m pretty sure that if GARP is satisfied, then by Afriat’s theorem, we have rationalisation.